이 게시물에서 LittleBird[1] 모델 구조 및 구현하는 방법에 대해서 살펴보도록 하겠습니다.
소개
LittleBird는 카카오엔터프라이즈가 직접 개발한 Sparse Attention Transformer 모델이며, BigBird[2]의 정확도를 유지하면서 메모리 사용량과 모델의 속도를 개선합니다. 간단하게 말씀 드리자면, LittleBird는 BigBird의 Sliding Window Attention과 LUNA[3]의 Pack & Unpack Attention을 합치고, ALiBi[4] 기반한 새로운 양방향 위치 정보를 표현하는 방법을 사용하는 모델입니다.
LittleBird 구조는 크게 LUNA, Sliding Window Attention, BiALiBi (양방향 ALiBi) 세 개의 부분으로 나눌 수 있고, LittleBird 공식을 살펴보면서 구현하는 방법을 설명해보도록 하겠습니다.
모델에 관련한 이론적인 부분 또는 학습하는 과정을 직접 논문을 통해 확인하시길 바랍니다.
공식
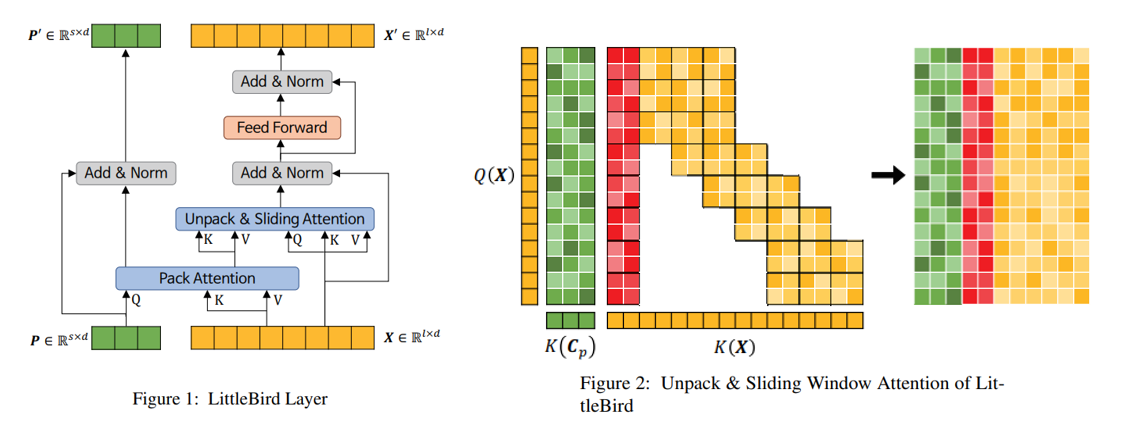
LittleBird 레이어
여기서 는 입력 시퀀스인데 와 는 각각 시퀀스 길이와 토큰 임베딩의 차원입니다. 는 Pack Attention의 projection 행렬인데, 는 축소할 시퀀스 길이입니다.
Attention
여기서 는 와 의 접합이며, 는 Unpack & Sliding Window Attention을 의미한다.
BiALiBi
는 Pack Attention의 위치 정보 표현하는 행렬이며, 는 크기 x 인 all-ones 행렬입니다. 는 BiALiBi로서, LittleBird 논문에서 Sliding Window Attention 위치 정보 표현하는 행렬로 사용합니다. , , 는 학습하는 파라미터입니다.
하이퍼 파라미터
모델 구현하기 전에 필수적인 하이퍼 파라미터들이 무엇인지 알면 좋을 것 같습니다. 앞으로의 코드 예시에서 사용할 예정입니다.
| 변수 | dtype | 기본값 | 설명 |
|---|---|---|---|
| seq_len | int | None | 입력 시퀀스 길이 |
| pack_len | int | None | projection 행렬 길이 |
| d_model | int | 512 | 임베딩 차원 |
| d_ff | int | 2048 | FeedForward layer 차원 |
| num_attention_heads | int | 8 | - |
| num_heads | int | 8 | num_attention_heads와 동일 |
| dropout_p | float | 0.1 | - |
| block_size | int | 64 | USWAttn 계산 시 블록 size |
| window_size | int | 3 | Sliding Window Attention 계산 시 window size |
LittleBird 레이어
숲을 보고 나무를 보라
LittleBirdModel을 탑다운(Top-Down) 방식으로 LittleBirdLayer 클래스부터 구현해봅시다. 위의 공식을 보시면, LittleBirdLayer는 LayerNorm 3 개, FeedForwardNetwork 하나, MultiHeadAttention 하나, 그리고 USWAttn 하나만으로 구성되어 있습니다. 아래와 같이 간단하게 LittleBirdLayer를 정의할 수 있습니다.
초기화
class LittleBirdLayer(nn.Module):
def __init__(...) -> None:
...
self.pack_attn = PackAttention(d_model, num_attention_heads)
self.unpack_sliding_attn = UnpackSlidingWindowAttention(
seq_len, pack_len, d_model, num_attention_heads, block_size
)
self.feed_forward = PositionwiseFeedForwardNetwork(d_model, d_ff, dropout_p)
self.pack_attn_layer_norm = nn.LayerNorm(d_model)
self.unpack_sliding_attn_layer_norm = nn.LayerNorm(d_model)
self.ffn_layer_norm = nn.LayerNorm(d_model)
Forward
계산을 각각의 레이어로 추상화했기 때문에 위의 공식에서 제시한대로 거의 똑같이 구현할 수 있습니다.
모델에는 여러 개의 LittleBird 레이어가 있고, 각각 다음 레이어에 와 를 입력하기 위해서 와 둘다 반환합니다.
def forward(
self,
P: torch.Tensor,
X: torch.Tensor,
attention_mask: torch.Tensor
):
Cp = self.pack_attn(P, X, attention_mask)
P0 = self.pack_attn_layer_norm(Cp + P)
Cx = self.unpack_sliding_attn(X, Cp, attention_mask)
A = self.unpack_sliding_attn_layer_norm(Cx + X)
X0 = self.ffn_layer_norm(self.feed_forward(A) + A)
return P0, X0
이제 더 깊이 들어가서 PositionwiseFeedForwardNetwork, PackAttention, 그리고 UnpackSlidingWindowAttention 구현해봅시다.
Feed Forward
모델에 non-linearity 추가하는 목적으로 (context)를 계산한 다음에 이를 FeedForward Network로 통과합니다.
이는 아래와 같이 Attention is all you need 논문에서 설명한대로 쉽게 구현할 수 있습니다.
class PositionwiseFeedForwardNetwork(nn.Module):
def __init__(...) -> None:
super(PositionwiseFeedForwardNetwork, self).__init__()
self.feed_forward = nn.Sequential(
nn.Linear(d_model, d_ff),
nn.Dropout(dropout_p),
nn.ReLU(),
nn.Linear(d_ff, d_model),
nn.Dropout(dropout_p),
)
def forward(self, inputs: torch.Tensor) -> torch.Tensor:
return self.feed_forward(inputs)
PackAttention
Pack & Unpack Attention의 Pack () 부분은 일반적인 Transformer 모델의 MultiHeadAttention과 동일하여 파이토치의 MultiHeadAttention 모듈을 사용하면 이 역시도 쉽게 구현할 수 있습니다.
class PackAttention(nn.Module):
def __init__(...):
super(PackAttention, self).__init__()
self.embed_dim = embed_dim
self.num_heads = num_heads
self.mha = nn.MultiheadAttention(
embed_dim=self.embed_dim, num_heads=self.num_heads, batch_first=True
)
def forward(self, P: torch.Tensor, X: torch.Tensor, attention_mask: torch.Tensor):
attn, _ = self.mha(P, X, X, attention_mask)
return attn
USWAttention
지금까지 모델 구현하는 데 딱히 어려움이 없었죠? 이제 난이도 조금 높혀서 Unpack & Sliding Window Attention 부분도 구현해볼까요?
초기화
Figure 2 또는 위의 공식에서 제시한 것처럼 UnpackSlidingWindowAttention이 Unpack Attention과 Global + Sliding Window Attention의 접합으로 구성돼 있고, 위치 정보를 표현하기 위해서 BiALiBi도 사용합니다. 이를 고려하여 UnpackSlidingWindowAttention 클래스의 초기화 함수를 아래와 같이 구현할 수 있습니다.
class UnpackSlidingWindowAttention(nn.Module):
def __init__(...):
super(UnpackSlidingWindowAttention, self).__init__()
# 하이퍼 파라미터
self.attn_head_size = int(dim / num_attention_heads)
self.num_attention_heads = num_attention_heads
self.block_size = block_size
self.seq_len = seq_len
self.pack_len = pack_len
# QKV 선형변환 레이어
self.Q = nn.Linear(dim, self.attn_head_size * num_attention_heads)
self.K = nn.Linear(dim, self.attn_head_size * num_attention_heads)
self.V = nn.Linear(dim, self.attn_head_size * num_attention_heads)
# 위치 정보 표현하는 BiALiBi 클래스
self.bialibi = BidirectionalALiBi(
self.num_attention_heads, self.seq_len
)
self.uniform_dist_mat = UniformDistanceMatrix(
self.num_attention_heads, self.block_size, self.seq_len, self.pack_len
)
self.register_buffer("middle_band_distance_indicies", None, persistent=False)
선형변환
맨위에 처음으로 scaling 계수 를 초기화하는데 multihead attention을 사용하므로 여기서 는 입니다.
그 다음으로 를 , , 와 그리고 를 및 의 내적을 계산하고, 이를 으로 나눈 다음에 마지막 두개의 차원이 과 에 해당하게끔 백터의 shape 변경합니다.
def forward(self, X, Cp, ...)
...
rsqrt_d = 1 / math.sqrt(self.attn_head_size)
batch_size, seq_len, dim = X.shape
query = transpose_for_scores(
self.Q(X), self.num_attention_heads, self.attn_head_size
) # bsz, head, seq_len, head_dim
key_x = transpose_for_scores(
self.K(X), self.num_attention_heads, self.attn_head_size
) # bsz, head, seq_len, head_dim
value_x = transpose_for_scores(
self.V(X), self.num_attention_heads, self.attn_head_size
) # bsz, head, seq_len, head_dim
key_Cp = transpose_for_scores(
self.K(Cp), self.num_attention_heads, self.attn_head_size
) # bsz, head, pack_len, head_dim
value_Cp = transpose_for_scores(
self.V(Cp), self.num_attention_heads, self.attn_head_size
) # bsz, head, pack_len, head_dim
...
transpose_for_scores 코드를 아래의 유틸리티 함수 부분에서 확인하실 수 있습니다.
Unpack Attention
이제 Unpack & Sliding Window Attention의 Unpack Attention 부분을 다뤄봅시다.
일반적으로 self-attention 계산 시 key와 query 백터의 내적을 통해 먼저 attention score 계산하고, 이를 정규화한 다음에 value 백터와의 내적을 통해 context 백터를 계산합니다. Unpack & Sliding Window Attention 사용하는 경우에 와 합친 백터과 와 의 합친 백터의 내적을 통해 Attention 계산합니다.
Sliding Window와 Unpack Attention 부분을 따로 처리하면 Unpack & Sliding Window Attention 쉽게 계산할 수 있습니다.
순서는 중요하지 않아 Unpack Attention 먼저 계산해볼까요?
코드
key_cp_attn[:] -= Dp 주목하시죠. 여기서는 context를 계산하기 전에 attention scores에서 uniform distance matrix를 뺍니다.
# Step 1 calculate the attention scores for the packed data
key_cp_attn = torch.matmul(query, key_Cp.transpose(2, 3))
key_cp_attn = key_cp_attn * rsqrt_d
key_cp_attn[:] -= Dp
key_cp_attn = F.softmax(key_cp_attn, dim=-1) # bsz, heads, seq_len, pack_len
packed_context = torch_bmm_nd(key_cp_attn, value_Cp, ndim=4)
Global + Sliding Window
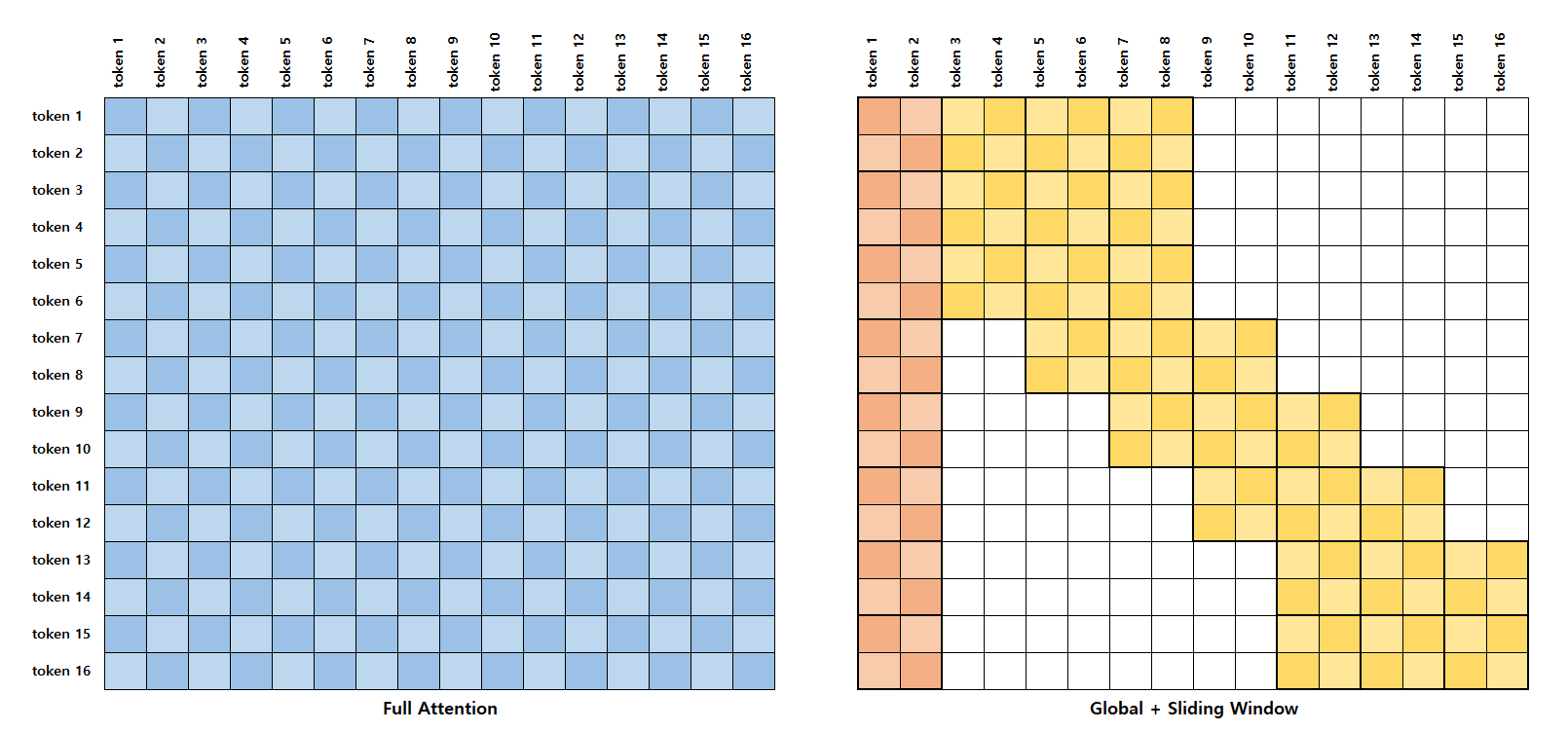
Figure 3: Full Attention과 Global + Sliding Window Attention 비교
Self-attention은 (quadratic complexity) 문제 때문에 512보다 더 긴 입력 시퀀스를 다루기 힘들지만, LittleBird 논문에서 나온 sparse attention 같은 방법을 사용하면 계산량이 줄어서 휠씬 긴 입력 시퀀스를 처리할 수 있습니다.
위의 이미지에서 self-attention와 sparse attention의 차이를 직접 눈으로 확인 하실 수 있습니다. 하얀색 네모들은 sparse attention 사용하는 경우에 계산하지 않는 attention score 입니다.
사실상, Unpack & Sliding Window attention 사용할 때도 보다 와 충분히 작을 때 시간 복잡도는 O(n) 입니다. 더 정확히 말하자면, self-attention의 시간 복잡도는 인데, Unpack & Sliding Window attention의 시간 복잡도는 입니다.
GPU에서 효율적으로 sparse multiplication을 수행할 수 없다는 것이 잘 알려져 있기 때문에, LittleBird 기반한 BigBird 논문의 저자들은 block sparse attention이란 attention의 key, value, query 백터들을 블록화해서 블록들끼리 attention을 계산하는 방법을 제안했습니다. 이를 토대로 LittleBird의 Global + Sliding Window Attention을 계산할 예정입니다.
입력 시퀀스 블록화

Figure 4: blockify example with a seq_len of 512 and a block_size of 64
view 메서드를 사용하면 아래와 같이 입력 시퀀스를 쉽게 블록화할 수 있습니다.
query_block = query.view(
batch_size,
self.num_attention_heads,
seq_len // self.block_size,
self.block_size,
-1,
)
key_x_block = key_x.view(
batch_size,
self.num_attention_heads,
seq_len // self.block_size,
self.block_size,
-1,
)
value_x_block = value_x.view(
batch_size,
self.num_attention_heads,
seq_len // self.block_size,
self.block_size,
-1,
)
첫 두 줄
첫 두 줄, 중간 줄, 마지막 줄 이렇게 총 세 단계로 attention score 계산할 예정입니다.
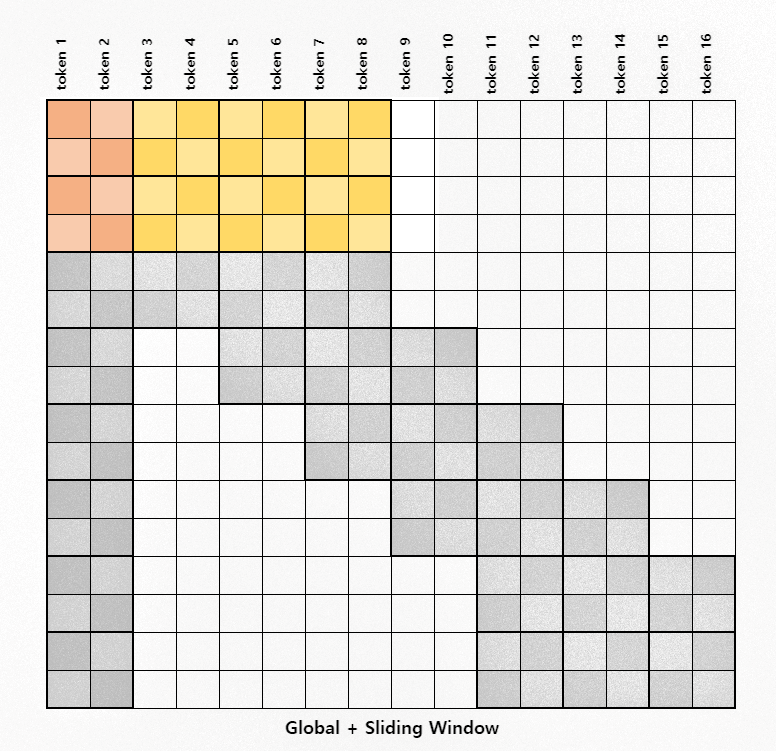
Figure 5: 첫 두 줄 Attention
Sliding window 계산 시 블록의 순서를 유지하기 위해 첫 두 줄, 중간 줄, 마지막 줄을 분리하여 계산합니다. 이는 다음 부분에서 더욱 명확해질 겁니다.
코드
이 단계에서 각 key, value, query 백터의 차원이 다음과 같습니다:
batch_size, attn_heads, num_blocks, block_size, head_dim = key_x_block.shape
먼저 첫 4개의 key와 value 벡터 블록, 첫 두개의 query 백터 블록 각각의 shape 변경해 묶습니다.
# Step 2.1. process the first two rows
first_two_rows_key_matrix = torch.cat(
[
key_x_block[:, :, 0],
key_x_block[:, :, 1],
key_x_block[:, :, 2],
key_x_block[:, :, 3],
],
dim=2,
)
first_two_rows_value_matrix = torch.cat(
[
value_x_block[:, :, 0],
value_x_block[:, :, 1],
value_x_block[:, :, 2],
value_x_block[:, :, 3],
],
dim=2,
)
first_two_query_blocks = torch.cat(
[query_block[:, :, 0], query_block[:, :, 1]], dim=2
)
그 다음으로는:
- key와 query 백터의 내적을 통해 attention score 계산
- attention score 정규화
- attention score에서 BiALiBi distance matrix 빼기
- attention mask
- softmax
- 그리고 마지막으로 attention score와 value 백터의 내적을 통해 context 계산
first_two_rows_attn = torch_bmm_nd_transpose(
first_two_query_blocks, first_two_rows_key_matrix, ndim=4
)
first_two_rows_attn *= rsqrt_d
first_two_rows_attn -= D[:, : self.block_size * 2, : self.block_size * 4]
first_two_rows_attn += (1.0 - self.mask_v[:, :, :self.block_size * 2, :self.block_size * 4]) * attn_penalty
first_two_rows_attn = F.softmax(first_two_rows_attn, dim=-1)
first_two_rows_context = torch_bmm_nd(
first_two_rows_attn, first_two_rows_value_matrix, ndim=4
)
마지막 단계에서 첫 두 줄, 중간 줄, 마지막 줄의 context 값들을 합쳐서 최종 context 백터를 생성합니다. 백터들을 블록 차원 기준으로 합쳐서 먼저 백터의 shape 변경해야 합니다.
_, __, ftr_3d, ftr_4d = first_two_rows_context.shape
first_two_rows_context = first_two_rows_context.view(
batch_size, self.num_attention_heads, 2, ftr_3d // 2, ftr_4d
) # bsz, heads, 2(blocks), block_size, block_size*4
슬라이딩 윈도우 (중간 줄)
BigBird 논문에서 제시한 sparse attention 방법을 사용해 중간 줄의 context 계산해 볼까요?
혹시나 저의 설명에 부족한 부분이 있으면 추가로 HuggingFace 블로그[5]에서 BigBird 논문 설명을 읽어보시고 부족한 부분을 보충하시는게 좋습니다!
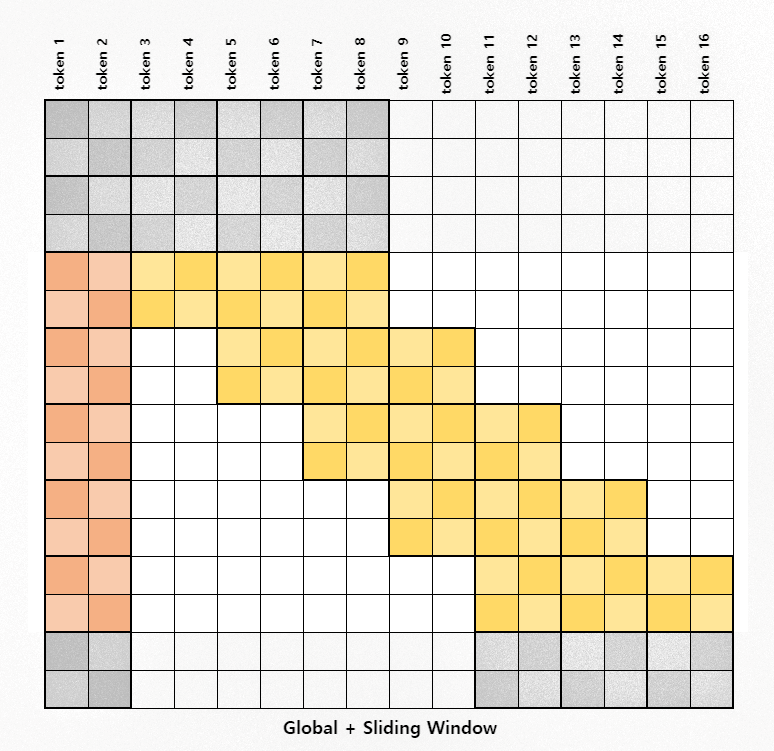
Figure 6: 중간 줄 attention
원리
블록된 key 백터를 2번 복사해서 돌리는데, 왼쪽으로 한번, 오른쪽으로 한번 백터를 돌립니다. 이 3개의 백터들을 합친 다음에 query 백터와의 내적을 계산하면 한번에 슬라이딩 윈도우에 있는 모든 토큰들의 attention score 계산할 수 있습니다.
블록된 key와 query 백터 내적을 계산하면 블록들끼리의 attention score만 계산이 됩니다.
아래의 이미지에서 나온 것처럼, 돌리지 않은 key 백터들과 query의 내적을 계산하면 대각선에 있는 토큰들끼리의 attention score가 계산이 됩니다. 왼쪽이나 오른쪽으로 돌린 key 백터과 query의 내적을 계산하면 대각선에서 왼쪽 또는 오른쪽에 하나 떨어져 있는 토큰들끼리의 attention score 계산이 됩니다.
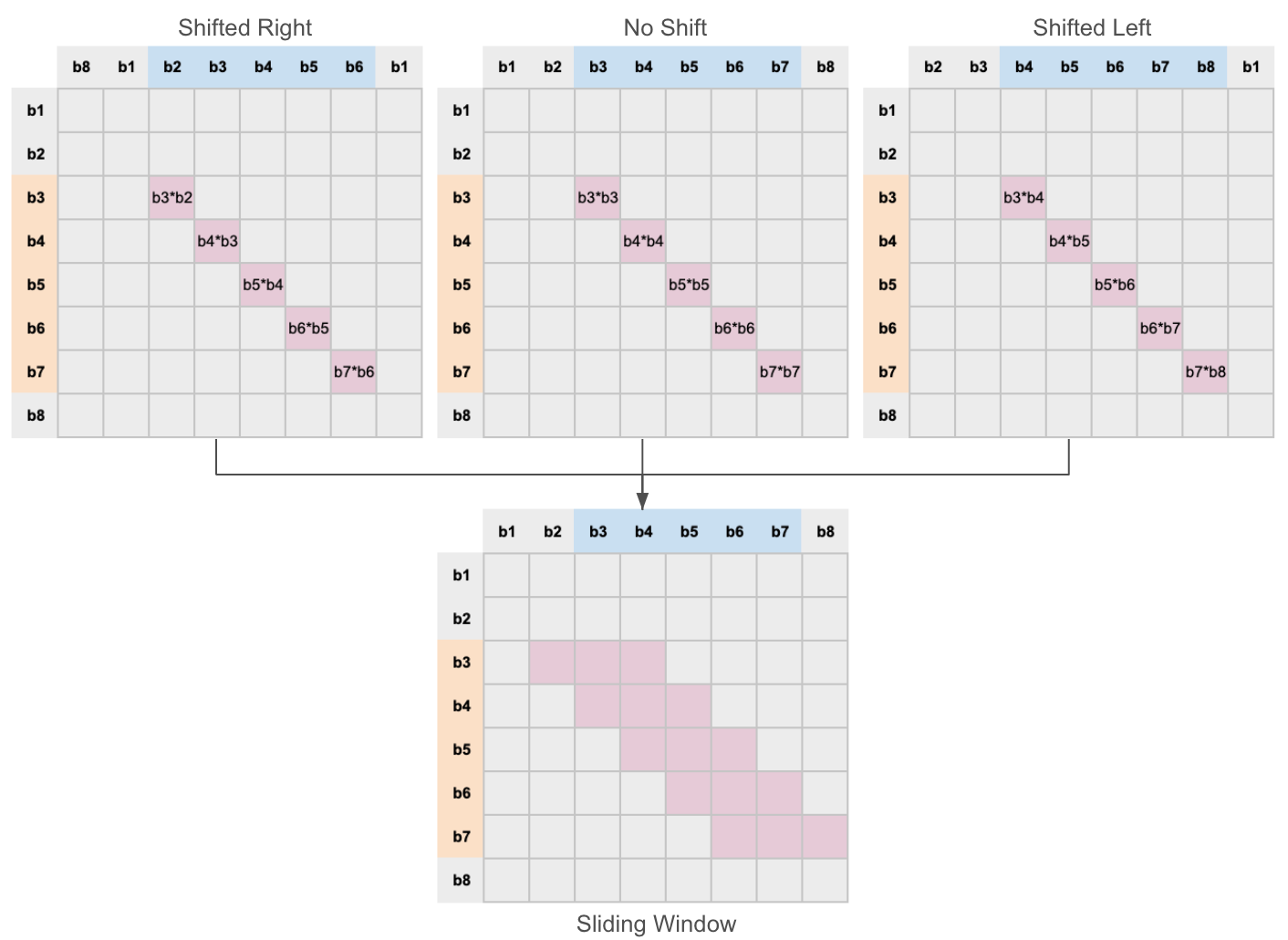
Figure 7: 슬라이딩 윈도우 attention 계산 시 들어가는 3가지의 단계
슬라이딩 윈도우 알고리즘
# step 2.2 calculate the middle part of the matrix
# the trick described in the bigbird paper is used
middle_band_key_matrix = torch.cat(
[
key_x_block[:, :, 1:-2], # roll back one
key_x_block[:, :, 2:-1],
key_x_block[:, :, 3:], # roll forward one
],
dim=3,
)
middle_band_value_matrix = torch.cat(
[
value_x_block[:, :, 1:-2], # roll back one
value_x_block[:, :, 2:-1],
value_x_block[:, :, 3:], # roll forward one
],
dim=3,
)
# get the diagnol
middle_band_sliding = torch_bmm_nd_transpose(
query_block[:, :, 2:-1], middle_band_key_matrix, ndim=5
)
middle_band_sliding += (1.0 - self.band_mask) * attn_penalty
글로벌 attention
추가적으로 중간 줄 처리할 때 첫번 째의 key 백터 블록과 모든 query 백터 블록들과의 내적을 통해 글로벌 attention을 계산합니다. 이는 위의 이미지에서 주황색으로 표시돼 있습니다. 글로벌 attention을 따로 계산한 뒤 슬라이딩 윈도우 context와 합칩니다.
# get the global
middle_band_global = torch.einsum(
"bhlqd,bhkd->bhlqk", query_block[:, :, 2:-1], key_x_block[:, :, 0]
)
middle_band_global += (1.0 - self.mask_block[:,2:-1,:].unsqueeze(3)) * attn_penalty
middle_band_attn = torch.cat([middle_band_global, middle_band_sliding], dim=-1)
middle_band_attn *= rsqrt_d
middle_band_attn -= self.get_middle_band_distances(D)
middle_band_attn = F.softmax(middle_band_attn, dim=-1)
middle_band_context = torch.einsum(
"bhlqk,bhkd->bhlqd",
middle_band_attn[:, :, :, :, : self.block_size],
value_x_block[:, :, 0],
)
middle_band_context += torch_bmm_nd(
middle_band_attn[:, :, :, :, self.block_size : 4 * self.block_size],
middle_band_value_matrix,
ndim=5,
)
마지막 줄
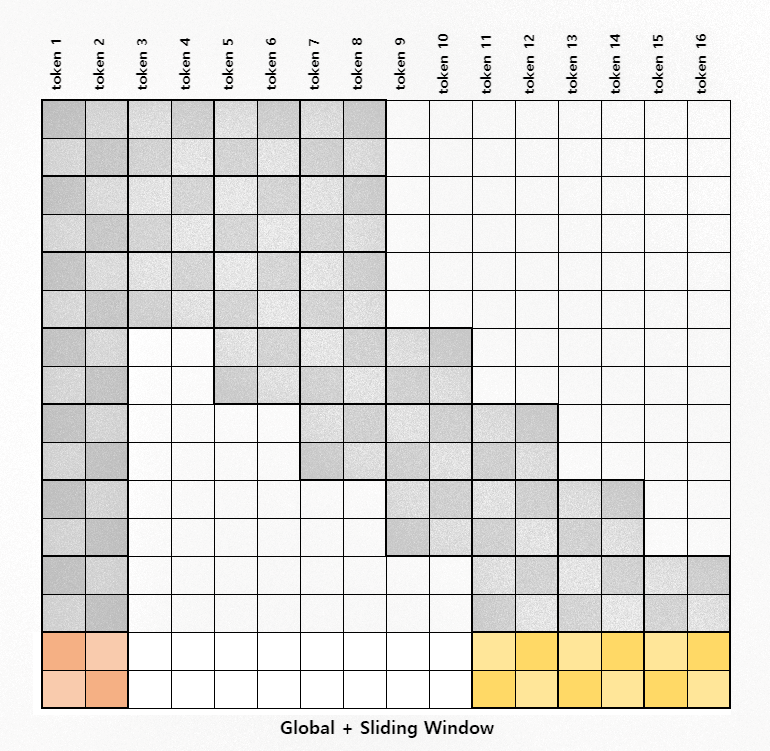
Figure 8: 마지막 줄 Attention
첫 두 줄과 비슷하게 계산하는데 첫 4개의 블록 대신 첫번째 블록과 마지막 3개의 블록들을 합쳐서 query와 내적을 통해 attention 계산합니다.
# calcualte the last row
last_row_key_matrix = torch.cat(
[
key_x_block[:, :, 0],
key_x_block[:, :, -3],
key_x_block[:, :, -2],
key_x_block[:, :, -1],
],
dim=2,
)
last_row_value_matrix = torch.cat(
[
value_x_block[:, :, 0],
value_x_block[:, :, -3],
value_x_block[:, :, -2],
value_x_block[:, :, -1],
],
dim=2,
)
last_row_attn = torch_bmm_nd_transpose(
query_block[:, :, -1], last_row_key_matrix, ndim=4
)
last_row_attn *= rsqrt_d
last_row_attn -= D[:, -self.block_size :, -self.block_size * 4 :]
last_row_attn = F.softmax(last_row_attn, dim=-1)
last_row_context = torch_bmm_nd(last_row_attn, last_row_value_matrix, ndim=4)
last_row_context.unsqueeze_(2)
마무리
마지막으로 첫 두 줄, 중간 줄, 마지막 줄의 context들을 합친 다음에 이의 백터 shape을 변경하고 unpack context와 더한 다음에 최종적으로 한번 더 마지막으로 최종 context 백터 shape을 변경합니다.
context_layer = torch.cat(
[first_two_rows_context, middle_band_context, last_row_context], dim=2
)
context_layer = context_layer.view(
(batch_size, self.num_attention_heads, seq_len, -1)
)
Cx = context_layer + packed_context
Cx = Cx.view(
batch_size, seq_len, self.num_attention_heads * self.attn_head_size
) * self.mask_v.squeeze(1)
return Cx
BiALiBi
BiALiBi distance 행렬을 만들기 위한 단계 세 가지 있습니다.
첫 번째로 행렬 대각선을 기준으로 대각선에서 각 요소의 거리에 해당하는 absolute distance 행렬을 생성합니다. 두 번째로 γ, β, α 가중치/파라미터 값들로 맨 위의 공식에서 나온 조건을 맞춰서 행렬 마스크 구축합니다.
마지막으로 absolute distance 행렬과 행렬 마스크를 성분곱 (element-wise multiplication)해서 BiALiBi 행렬을 만들 수 있습니다.
1. distance 행렬 초기화
row_i = torch.arange(self.seq_len, dtype=torch.float32)
col_i = torch.arange(self.seq_len, dtype=torch.float32).unsqueeze(-1)
distances = (row_i - col_i).abs()
distances
tensor([[0, 1, 2, 3, 4, 5],
[1, 0, 1, 2, 3, 4],
[2, 1, 0, 1, 2, 3],
[3, 2, 1, 0, 1, 2],
[4, 3, 2, 1, 0, 1],
[5, 4, 3, 2, 1, 0]], dtype=torch.int32)
2. gamma(γ) 및 beta(β) 마스크
gamma_mask = torch.triu(torch.ones_like(self.distances), diagonal=1)
gamma_mask *= self.gamma.view(-1, 1, 1)
gamma_mask
tensor([[[0.0000, 0.4540, 0.4540, 0.4540, 0.4540, 0.4540],
[0.0000, 0.0000, 0.4540, 0.4540, 0.4540, 0.4540],
[0.0000, 0.0000, 0.0000, 0.4540, 0.4540, 0.4540],
[0.0000, 0.0000, 0.0000, 0.0000, 0.4540, 0.4540],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.4540],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]]],
grad_fn=<MulBackward0>)
beta_mask = torch.tril(torch.ones_like(self.distances), diagonal=-1)
beta_mask *= self.beta.view(-1, 1, 1)
beta_mask
tensor([[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.9392, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.9392, 0.9392, 0.0000, 0.0000, 0.0000, 0.0000],
[0.9392, 0.9392, 0.9392, 0.0000, 0.0000, 0.0000],
[0.9392, 0.9392, 0.9392, 0.9392, 0.0000, 0.0000],
[0.9392, 0.9392, 0.9392, 0.9392, 0.9392, 0.0000]]],
grad_fn=<MulBackward0>)
3. Gamma와 Beta 마스크를 더한 다음에 마스크에 alpha(α)를 삽입
mask = beta_mask + gamma_mask
# step 4: set the alphas
mask[:, 0, :] = 1.0
mask[:, :, 0] = 1.0
mask[:, 1:, 0] *= self.alpha.unsqueeze(1)
mask[:, 0, 1:] *= self.alpha.unsqueeze(1)
mask[:, 0, 0] *= 0.0
tensor([[[0.0000, 0.7959, 0.7959, 0.7959, 0.7959, 0.7959],
[0.7959, 0.0000, 0.4540, 0.4540, 0.4540, 0.4540],
[0.7959, 0.9392, 0.0000, 0.4540, 0.4540, 0.4540],
[0.7959, 0.9392, 0.9392, 0.0000, 0.4540, 0.4540],
[0.7959, 0.9392, 0.9392, 0.9392, 0.0000, 0.4540],
[0.7959, 0.9392, 0.9392, 0.9392, 0.9392, 0.0000]]],
grad_fn=<CopySlices>)
마지막으로 마스크와 absolute distance 행렬을 성분곱 (element-wise multiplication)해서 BiALiBi 행렬을 만듭니다.
self.distances * mask
tensor([[[0.0000, 0.2621, 0.5243, 0.7864, 1.0486, 1.3107],
[0.2621, 0.0000, 0.6620, 1.3239, 1.9859, 2.6478],
[0.5243, 0.4262, 0.0000, 0.6620, 1.3239, 1.9859],
[0.7864, 0.8524, 0.4262, 0.0000, 0.6620, 1.3239],
[1.0486, 1.2787, 0.8524, 0.4262, 0.0000, 0.6620],
[1.3107, 1.7049, 1.2787, 0.8524, 0.4262, 0.0000]]],
grad_fn=<MulBackward0>)
유틸리티 함수
아래의 함수들은 HuggingFace 저장소에 있는 BigBird 모델 코드에서 가져와 LittleBird에서 쓸 수 있게 살짝 수정한 함수들입니다.
def torch_bmm_nd_transpose(inp_1, inp_2, ndim=None):
"""Fast nd matrix multiplication with transpose"""
# faster replacement of torch.einsum (bhqd,bhkd->bhqk)
return torch.bmm(
inp_1.reshape((-1,) + inp_1.shape[-2:]),
inp_2.reshape((-1,) + inp_2.shape[-2:]).transpose(1, 2),
).view(inp_1.shape[: ndim - 2] + (inp_1.shape[ndim - 2], inp_2.shape[ndim - 2]))
def torch_bmm_nd(inp_1, inp_2, ndim=None):
"""Fast nd matrix multiplication"""
# faster replacement of torch.einsum ("bhqk,bhkd->bhqd")
return torch.bmm(
inp_1.reshape((-1,) + inp_1.shape[-2:]), inp_2.reshape((-1,) + inp_2.shape[-2:])
).view(inp_1.shape[: ndim - 2] + (inp_1.shape[ndim - 2], inp_2.shape[ndim - 1]))
def transpose_for_scores(x, num_attn_head, attn_head_size):
new_x_shape = x.size()[:-1] + (num_attn_head, attn_head_size)
x = x.view(*new_x_shape)
return x.permute(0, 2, 1, 3)
기타
읽어주셔서 감사합니다.
전체 소스코드 Github에서 확인하실 수 있습니다!
만약에 질문이 있으시거나 설명에 대해 잘못된 부분이 있으면 위의 Github 저�장소에 이슈를 올려 알려주시면 잘못된 부분을 수정하도록 하겠습니다! 😊
참조
- [1] LittleBird: Efficient Faster & Longer Transformer for Question Answering
- [2] Big Bird: Transformers for Longer Sequences
- [3] Luna: Linear Unified Nested Attention
- [4] Train Short, Test Long: Attention with Linear Biases Enables Input Length Extrapolation
- [5] Understanding BigBird's Block Sparse Attention